Part 3, Topic 2: Recovering AES Key from a Single Bit of Data¶
NOTE: This lab references some (commercial) training material on ChipWhisperer.io. You can freely execute and use the lab per the open-source license (including using it in your own courses if you distribute similarly), but you must maintain notice about this source location. Consider joining our training course to enjoy the full experience.
Let's do a basic demo to recover a single bit of data from an internal state of an AES implementation, and see how far we can take our attack.
SUMMARY: This lab will take you through the associated information about how to recover an AES key from a single "bit" of leakage. We already saw how power analysis can be used to understand device leakage, but how does that mean we can recover cryptographic information?
LEARNING OUTCOMES:
- Understand some basics of the AES algorithm.
- See how a single bit of leakage can translate to a full key reveal.
- See how to sort and ranking lists.
1. AES Refresher¶
You'll be an expert at AES (or recognizing AES figures) by the end of this course! Remember that the input data flow for AES is something like this:
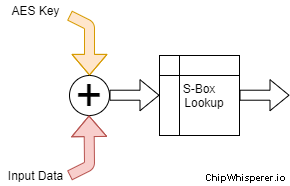
Where the input data is XOR'd with a key byte, and then passed through an S-Box. First, let's build our AES model. I'm going to make your life slightly easier by giving you the S-Box data:
sbox = [
# 0 1 2 3 4 5 6 7 8 9 a b c d e f
0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76, # 0
0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0, # 1
0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15, # 2
0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75, # 3
0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84, # 4
0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf, # 5
0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8, # 6
0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2, # 7
0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73, # 8
0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb, # 9
0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79, # a
0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08, # b
0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a, # c
0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e, # d
0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf, # e
0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16 # f
]
Alright - that should be enough for you to build a simple function that XORs a secret key value with the input data, and then performs a lookup in the above table. Before you continue, modify the following code block to implement the correct function:
1.1 aes_internal()¶
def aes_internal(inputdata, key):
return sbox[inputdata ^ key]
With that working - go ahead and run the following test vectors. If the values are not as expected, check your implementation. If the following executes without error, then go onto the next part.
#Simple test vectors - if you get the check-mark printed all OK.
assert(aes_internal(0xAB, 0xEF) == 0x1B)
assert(aes_internal(0x22, 0x01) == 0x26)
print("✔️ OK to continue!")
✔️ OK to continue!
Finally - we'll make a new function which doesn't expose the key. The following function has some hard-coded key. You can change this key byte if you'd like, and see it recovered at a later step!
1.2 aes_secret()¶
def aes_secret(inputdata):
secret_key = 0xEF
return aes_internal(secret_key, inputdata)
At this point, we can get the value of some internal part of the AES algorithm. For our first attack, we're going to assume that we can't observe this entire value. Let's just observe a single bit of the value - imagine that someone put a probe down inside the chip to get this. We can do this by simply throwing away all the other data besides a single bit, and only expose that single bit to the observer.
Let's build the watcher now.
2. AES Watcher¶
The watcher is going to observe a single bit of data. We'll need to build lists of input we feed to the algorithm (we're just going to send in 1000 random bytes that get 'encrypted'), as well as lists to hold our observation. In case you're still picking up Python, here are a few handy little things you might need in this section:
##Some Python hints/useful functions:
# You can use this function to generate the random data
import random
random.randint(0, 255)
# List comprehension can be used to shovel data through a function
def somefunc(a):
return a + 4
input_data = [1,2,5,6]
output_data = [somefunc(a) for a in input_data]
# You can use this while ignoring the index variable too
output_data = [somefunc(random.randint(0,255)) for _ in range(0, 1000)]
Your first objective is to build a list of data you are encrypted with aes_secret(). This should be a 1000-item random number which ranges from 0 to 255. Call it input_data. For example if you print the input_data list it could look like [2, 49, 0, 212, 94, 255, ... , 7], where there are 1000 elements in total. Fill in the following code to make a list of the 1000 random values in the correct range (see hints above if you need some Python syntax).
2.1 Generation of input_data¶
input_data = [random.randint(0,255) for _ in range(0, 1000)]
#Simple test vectors - if you get the check-mark printed all OK.
assert(len(input_data) == 1000)
#assert(max(input_data) == 0xFF) #Possibly not true for random variables (re-run if you get an error)
#assert(min(input_data) == 0x00) #Possibly not true for random variables (re-run if you get an error)
print("✔️ OK to continue!")
✔️ OK to continue!
Now, feed all those inputs through the aes_secret function. Because this is a secret function we are only going to observe a single bit of output (the 'leakage'). The following will perform the encryptions and mask off all but the lowest bit for you, and build a new array called leaked_data which contains just the 1 or 0 status of the lowest bit.
2.2 Definition of leaked_data¶
leaked_data = [(aes_secret(a) & 0x01) for a in input_data]
If you run the following too cells, it will then print some of the data so you can see the sequence of 1 and 0.
print(leaked_data)
[0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0]
You can also plot for example the patterns of 1's and 0's - this gets pretty squashed, so let's just look at a few hundred transitions:
import matplotlib.pylab as plt
plt.plot(leaked_data[0:200])
plt.show()
Do you think we'll be able to get something useful out of this? Let's attack it to find out.
3. AES Guesser¶
The attack is pretty simple. Let's just use our model of the device (we know what the encryption does after all, just not the secret key). And we'll feed in the observed data for each possible value of the key. And then we can observe how many (if any) of the keys result in the observation and simulation matching each other. If the observation and simulation match, this suggets our simulation is running in the same "setup" as the implementation we are attacking!
First, build a function to count the number of elements in a list that match between two lists (that is - same value of the element at the same list index). An easy way is to just iterate through the number of elements in the list and count the number that are the same. Fill in the following - there is already some bounds checking code to get you started.
3.1 num_same()¶
def num_same(a, b):
if len(a) != len(b):
raise ValueError("Arrays must be same length!")
if max(a) != max(b):
raise ValueError("Arrays max() should be the same!")
#Count how many list items match up
same = 0
for i, _ in enumerate(a):
if a[i] == b[i]:
same += 1
return same
#Simple test vectors - if you get the check-mark printed all OK.
assert(num_same([0,1,0,1,1,1,1,0], [0,1,0,1,1,1,1,0]) == 8)
assert(num_same([1,1,1,0,0,0,0,0], [0,1,0,1,1,1,1,0]) == 2)
assert(num_same([1, 0], [0, 1]) == 0)
print("✔️ OK to continue!")
✔️ OK to continue!
The next block is the most important. You'll need to "apply" the leakage function - that is for each known input byte, pass it through the aes_internal(input_data, key_guess) function. The value of key_guess is just integers in [0x00, 0x01,...,0xFF] - aka every possible value of the key byte. We'll compare the number of matching bits between our observed (leaked) data bit and the hypothetical data bit.
3.2 Guessing Loop¶
for guess in range(0, 256):
#Get a hypothetical leakage list - use aes_internal(guess, input_byte) and mask off to only get value of lowest bit.
#You'll need to make this into a list as wel.
hypothetical_leakage = [aes_internal(guess, input_byte) & 0x01 for input_byte in input_data]
#Use our function
same_count = num_same(hypothetical_leakage, leaked_data)
#Print for debug
print("Guess {:02X}: {:4d} bits same".format(guess, same_count))
Guess 00: 483 bits same Guess 01: 406 bits same Guess 02: 487 bits same Guess 03: 519 bits same Guess 04: 444 bits same Guess 05: 467 bits same Guess 06: 448 bits same Guess 07: 497 bits same Guess 08: 503 bits same Guess 09: 494 bits same Guess 0A: 493 bits same Guess 0B: 502 bits same Guess 0C: 533 bits same Guess 0D: 551 bits same Guess 0E: 531 bits same Guess 0F: 516 bits same Guess 10: 494 bits same Guess 11: 516 bits same Guess 12: 430 bits same Guess 13: 500 bits same Guess 14: 521 bits same Guess 15: 519 bits same Guess 16: 521 bits same Guess 17: 547 bits same Guess 18: 497 bits same Guess 19: 470 bits same Guess 1A: 459 bits same Guess 1B: 516 bits same Guess 1C: 493 bits same Guess 1D: 445 bits same Guess 1E: 467 bits same Guess 1F: 492 bits same Guess 20: 477 bits same Guess 21: 502 bits same Guess 22: 448 bits same Guess 23: 461 bits same Guess 24: 541 bits same Guess 25: 472 bits same Guess 26: 529 bits same Guess 27: 448 bits same Guess 28: 518 bits same Guess 29: 492 bits same Guess 2A: 495 bits same Guess 2B: 505 bits same Guess 2C: 445 bits same Guess 2D: 517 bits same Guess 2E: 518 bits same Guess 2F: 508 bits same Guess 30: 516 bits same Guess 31: 502 bits same Guess 32: 461 bits same Guess 33: 501 bits same Guess 34: 518 bits same Guess 35: 484 bits same Guess 36: 481 bits same Guess 37: 547 bits same Guess 38: 507 bits same Guess 39: 459 bits same Guess 3A: 469 bits same Guess 3B: 516 bits same Guess 3C: 478 bits same Guess 3D: 575 bits same Guess 3E: 457 bits same Guess 3F: 492 bits same Guess 40: 518 bits same Guess 41: 517 bits same Guess 42: 494 bits same Guess 43: 461 bits same Guess 44: 480 bits same Guess 45: 511 bits same Guess 46: 521 bits same Guess 47: 473 bits same Guess 48: 469 bits same Guess 49: 468 bits same Guess 4A: 519 bits same Guess 4B: 504 bits same Guess 4C: 479 bits same Guess 4D: 520 bits same Guess 4E: 488 bits same Guess 4F: 459 bits same Guess 50: 513 bits same Guess 51: 519 bits same Guess 52: 482 bits same Guess 53: 556 bits same Guess 54: 486 bits same Guess 55: 520 bits same Guess 56: 475 bits same Guess 57: 466 bits same Guess 58: 488 bits same Guess 59: 469 bits same Guess 5A: 473 bits same Guess 5B: 476 bits same Guess 5C: 501 bits same Guess 5D: 517 bits same Guess 5E: 474 bits same Guess 5F: 487 bits same Guess 60: 484 bits same Guess 61: 513 bits same Guess 62: 553 bits same Guess 63: 521 bits same Guess 64: 486 bits same Guess 65: 515 bits same Guess 66: 555 bits same Guess 67: 458 bits same Guess 68: 488 bits same Guess 69: 500 bits same Guess 6A: 505 bits same Guess 6B: 543 bits same Guess 6C: 499 bits same Guess 6D: 565 bits same Guess 6E: 467 bits same Guess 6F: 461 bits same Guess 70: 471 bits same Guess 71: 466 bits same Guess 72: 519 bits same Guess 73: 523 bits same Guess 74: 507 bits same Guess 75: 506 bits same Guess 76: 448 bits same Guess 77: 482 bits same Guess 78: 416 bits same Guess 79: 490 bits same Guess 7A: 527 bits same Guess 7B: 485 bits same Guess 7C: 443 bits same Guess 7D: 511 bits same Guess 7E: 484 bits same Guess 7F: 458 bits same Guess 80: 545 bits same Guess 81: 544 bits same Guess 82: 579 bits same Guess 83: 466 bits same Guess 84: 556 bits same Guess 85: 528 bits same Guess 86: 462 bits same Guess 87: 558 bits same Guess 88: 440 bits same Guess 89: 583 bits same Guess 8A: 555 bits same Guess 8B: 505 bits same Guess 8C: 464 bits same Guess 8D: 542 bits same Guess 8E: 517 bits same Guess 8F: 517 bits same Guess 90: 451 bits same Guess 91: 568 bits same Guess 92: 558 bits same Guess 93: 525 bits same Guess 94: 479 bits same Guess 95: 511 bits same Guess 96: 501 bits same Guess 97: 435 bits same Guess 98: 494 bits same Guess 99: 538 bits same Guess 9A: 546 bits same Guess 9B: 420 bits same Guess 9C: 429 bits same Guess 9D: 465 bits same Guess 9E: 530 bits same Guess 9F: 470 bits same Guess A0: 522 bits same Guess A1: 457 bits same Guess A2: 486 bits same Guess A3: 536 bits same Guess A4: 531 bits same Guess A5: 486 bits same Guess A6: 560 bits same Guess A7: 501 bits same Guess A8: 546 bits same Guess A9: 541 bits same Guess AA: 451 bits same Guess AB: 505 bits same Guess AC: 489 bits same Guess AD: 540 bits same Guess AE: 431 bits same Guess AF: 463 bits same Guess B0: 550 bits same Guess B1: 469 bits same Guess B2: 504 bits same Guess B3: 577 bits same Guess B4: 510 bits same Guess B5: 523 bits same Guess B6: 485 bits same Guess B7: 516 bits same Guess B8: 568 bits same Guess B9: 536 bits same Guess BA: 526 bits same Guess BB: 459 bits same Guess BC: 452 bits same Guess BD: 476 bits same Guess BE: 467 bits same Guess BF: 456 bits same Guess C0: 451 bits same Guess C1: 456 bits same Guess C2: 508 bits same Guess C3: 479 bits same Guess C4: 496 bits same Guess C5: 556 bits same Guess C6: 525 bits same Guess C7: 503 bits same Guess C8: 500 bits same Guess C9: 554 bits same Guess CA: 440 bits same Guess CB: 530 bits same Guess CC: 501 bits same Guess CD: 527 bits same Guess CE: 524 bits same Guess CF: 550 bits same Guess D0: 470 bits same Guess D1: 525 bits same Guess D2: 517 bits same Guess D3: 455 bits same Guess D4: 420 bits same Guess D5: 548 bits same Guess D6: 479 bits same Guess D7: 556 bits same Guess D8: 539 bits same Guess D9: 482 bits same Guess DA: 518 bits same Guess DB: 442 bits same Guess DC: 475 bits same Guess DD: 498 bits same Guess DE: 502 bits same Guess DF: 511 bits same Guess E0: 506 bits same Guess E1: 546 bits same Guess E2: 510 bits same Guess E3: 471 bits same Guess E4: 504 bits same Guess E5: 454 bits same Guess E6: 480 bits same Guess E7: 471 bits same Guess E8: 536 bits same Guess E9: 463 bits same Guess EA: 521 bits same Guess EB: 502 bits same Guess EC: 533 bits same Guess ED: 522 bits same Guess EE: 499 bits same Guess EF: 1000 bits same Guess F0: 484 bits same Guess F1: 500 bits same Guess F2: 441 bits same Guess F3: 473 bits same Guess F4: 524 bits same Guess F5: 491 bits same Guess F6: 478 bits same Guess F7: 530 bits same Guess F8: 462 bits same Guess F9: 539 bits same Guess FA: 458 bits same Guess FB: 484 bits same Guess FC: 530 bits same Guess FD: 415 bits same Guess FE: 475 bits same Guess FF: 529 bits same
If your key guess is wrong, about half of the guesses should be wrong. Looking through the list, you'll see that most of the "bits same" numbers will be around 500. But scroll down to the correct key value (should be 0xEF if you haven't changed it earlier). With any luck, that number should be fully correct - 1000 matching bits. This is only possible if the internal "secret key" byte matches the observed key.
3.3 argsort background¶
Now a handy thing to do will be to sort based on the values by number of correct bits so we don't have to look through that list. An easy way to do this is with numpy.argsort - this returns the indicies that would sort the list. To start small, take the following for example:
import numpy as np
count_list = [2, 7, 24, 4, 5]
np.argsort(count_list)
array([0, 3, 4, 1, 2])
This should return [0, 3, 4, 1, 2] - you can cast the above to list() type if you want to get rid of the array() type around it.
Inspecting the above, notice that this is the position of each from lowest to highest. We can reverse this to give us a highest to lowest sort instead:
import numpy as np
count_list = [2, 7, 24, 4, 5]
np.argsort(count_list)[::-1]
array([2, 1, 4, 3, 0])
Taking your previous code, simply make a new list which contains the number of elements which are the same, where the list index is the key guess. As a rough outline, see the following (you'll need to add back in your hypothetical code):
3.4 Guessing loop with sort¶
import numpy as np
guess_list = [0] * 256
for guess in range(0, 256):
#Get a hypothetical leakage list - use aes_internal(guess, input_byte) and mask off to only get value of lowest bit
hypothetical_leakage = [aes_internal(guess, input_byte) & 0x01 for input_byte in input_data]
#Use our function
same_count = num_same(hypothetical_leakage, leaked_data)
#Track the number of correct bits
guess_list[guess] = same_count
#Use np.argsort to generate a list of indicies from low to high, then [::-1] to reverse the list to get high to low.
sorted_list = np.argsort(guess_list)[::-1]
#Print top 5 only
for guess in sorted_list[0:5]:
print("Key Guess {:02X} = {:04d} matches".format(guess, guess_list[guess]))
Key Guess EF = 1000 matches Key Guess 89 = 0583 matches Key Guess 82 = 0579 matches Key Guess B3 = 0577 matches Key Guess 3D = 0575 matches
In this case we know that bit '0' was the leakage. What if we didn't know that? Imagine putting our needle down onto the internal bus, but we aren't sure what bit we touched.
Luckily we can easily test that. To do so, we'll need to adjust our leakage function to take in a bit number that is leaking. First, define a function which returns the value of a bit being 1 or 0:
3.5 get_bit()¶
def get_bit(data, bit):
if data & (1<<bit):
return 1
else:
return 0
assert(get_bit(0xAA, 7) == 1)
assert(get_bit(0xAA, 0) == 0)
assert(get_bit(0x00, 7) == 0)
print("✔️ OK to continue!")
✔️ OK to continue!
Now let's make a slightly fancier leakage function with it:
def aes_leakage_guess(keyguess, inputdata, bit):
return get_bit(aes_internal(keyguess, inputdata), bit)
assert(aes_leakage_guess(0xAB, 0x22, 4) == 0)
assert(aes_leakage_guess(0xAB, 0x22, 3) == 0)
assert(aes_leakage_guess(0xAB, 0x22, 2) == 1)
assert(aes_leakage_guess(0xAB, 0x22, 1) == 1)
assert(aes_leakage_guess(0xAB, 0x22, 0) == 1)
print("✔️ OK to continue!")
✔️ OK to continue!
Finally, finish off this loop by adding your leakage function into it. Running the loop should print results for each bit option - hopefully you see that only the matching bit shows the full number of matches. If you want to try a different leaky bit, you'll then need to go back up to the actual secret observation to make the leak happen from a different bit. But you can see the following code makes no assumptions about 'bit 0' being the leaky one - it will work with any other bit leaking now.
3.6 Bitwise Guessing Loop¶
for bit_guess in range(0, 8):
guess_list = [0] * 256
print("Checking bit {:d}".format(bit_guess))
for guess in range(0, 256):
#Get a hypothetical leakage for guessed bit (ensure returns 1/0 only)
#Use bit_guess as the bit number, guess as the key guess, and data from input_data
hypothetical_leakage = [aes_leakage_guess(guess, input_byte, bit_guess) for input_byte in input_data]
#Use our function
same_count = num_same(hypothetical_leakage, leaked_data)
#Track the number of correct bits
guess_list[guess] = same_count
sorted_list = np.argsort(guess_list)[::-1]
#Print top 5 only
for guess in sorted_list[0:5]:
print("Key Guess {:02X} = {:04d} matches".format(guess, guess_list[guess]))
Checking bit 0
Key Guess EF = 1000 matches Key Guess 89 = 0583 matches Key Guess 82 = 0579 matches Key Guess B3 = 0577 matches Key Guess 3D = 0575 matches Checking bit 1
Key Guess 21 = 0584 matches Key Guess C0 = 0577 matches Key Guess 9F = 0573 matches Key Guess E2 = 0569 matches Key Guess 15 = 0568 matches Checking bit 2 Key Guess 7D = 0592 matches Key Guess 59 = 0579 matches Key Guess 84 = 0579 matches Key Guess 17 = 0571 matches Key Guess 19 = 0570 matches Checking bit 3
Key Guess 22 = 0575 matches Key Guess 25 = 0572 matches Key Guess A8 = 0571 matches Key Guess 06 = 0571 matches Key Guess 8A = 0571 matches Checking bit 4 Key Guess E5 = 0585 matches Key Guess 40 = 0573 matches Key Guess 09 = 0571 matches Key Guess E7 = 0568 matches Key Guess BF = 0568 matches Checking bit 5
Key Guess D3 = 0581 matches Key Guess C9 = 0577 matches Key Guess AD = 0575 matches Key Guess E4 = 0568 matches Key Guess 66 = 0567 matches Checking bit 6 Key Guess C3 = 0592 matches Key Guess FB = 0588 matches Key Guess 6B = 0585 matches Key Guess 03 = 0574 matches Key Guess 01 = 0571 matches Checking bit 7
Key Guess 96 = 0586 matches Key Guess 7A = 0579 matches Key Guess F1 = 0573 matches Key Guess EB = 0572 matches Key Guess BE = 0570 matches
🥳🥳🥳🥳🥳🥳🥳🥳🥳🥳🥳🥳🥳 Congrats - you did it!!!!
This all assumed you get some way to observe the value of the bit - in our next act, we'll see how power analysis gives us the ability to observe a given bit.
4. Bonus: Adding Noise and Plotting Success Rates¶
Are you not satisified by your attack? Why not see what happens when you add some noise into the equation?
Remember this simple leakage from earlier:
leaked_data = [(aes_secret(a) & 0x01) for a in input_data]
This relied on another function aes_secret(), which we could define as such to return incorrect responses sometimes:
import random
def aes_secret(inputdata):
secret_key = 0xEF
correct = aes_internal(secret_key, inputdata)
if random.randint(0, 100) < 10:
return correct
else:
return 0
What happens now? While it should take more guesses to get the correct byte out. In fact, we could even make a plot of the percentage of returned wrong results, and how many observations it took to get the correct answer.
The end result should look something like this:
Give it a try. If you get stuck of course you can check out the solution lab too.
import random
def aes_secret_chance(inputdata, chance_correct):
secret_key = 0xEF
correct = aes_internal(secret_key, inputdata)
if random.randint(0, 100) <= chance_correct:
return correct
else:
return 0
def num_same(a, b):
if len(a) != len(b):
raise ValueError("Arrays must be same length!")
#Count how many list items match up
same = 0
for i, _ in enumerate(a):
if a[i] == b[i]:
same += 1
return same
#This sets the percentage of correct observations
chances_to_try = range(20, 105, 5)
traces_needed = []
for chance_correct in chances_to_try:
leaked_data = [(aes_secret_chance(a, chance_correct) & 0x01) for a in input_data]
#Try for number of traces
for traces in range(1, len(input_data), 1):
guess_list = [0] * 256
for guess in range(0, 256):
#Get a hypothetical leakage list - use aes_internal(guess, input_byte) and mask off to only get value of lowest bit
hypothetical_leakage = [aes_internal(guess, input_byte) & 0x01 for input_byte in input_data[0:traces]]
#Use our function
same_count = num_same(hypothetical_leakage, leaked_data[0:traces])
#Track the number of correct bits
guess_list[guess] = same_count
#Use np.argsort to generate a list of indicies from low to high, then [::-1] to reverse the list to get high to low.
sorted_list = np.argsort(guess_list)[::-1]
if sorted_list[0] == 0xEF:
print("Found key at %d %% correct data with %d encryptions"%(chance_correct, traces))
traces_needed.append(traces)
break
if sorted_list[0] != 0xEF:
raise ValueError("Failed to find answer for %d %% - need more traces"%(chance_correct))
Found key at 20 % correct data with 51 encryptions
Found key at 25 % correct data with 270 encryptions
Found key at 30 % correct data with 95 encryptions
Found key at 35 % correct data with 85 encryptions
Found key at 40 % correct data with 108 encryptions Found key at 45 % correct data with 44 encryptions Found key at 50 % correct data with 10 encryptions Found key at 55 % correct data with 24 encryptions
Found key at 60 % correct data with 40 encryptions Found key at 65 % correct data with 9 encryptions Found key at 70 % correct data with 22 encryptions Found key at 75 % correct data with 16 encryptions Found key at 80 % correct data with 9 encryptions Found key at 85 % correct data with 9 encryptions Found key at 90 % correct data with 11 encryptions Found key at 95 % correct data with 9 encryptions Found key at 100 % correct data with 9 encryptions
import matplotlib.pylab as plt
plt.figure(figsize=(6,3), dpi=150)
plt.plot(chances_to_try, traces_needed)
plt.title('Guesses for Single Bit Observation')
plt.xlabel('% Chance of Correct Observation')
plt.ylabel('Encryptions To Recover Key')
Text(0, 0.5, 'Encryptions To Recover Key')
NO-FUN DISCLAIMER: This material is Copyright (C) NewAE Technology Inc., 2015-2020. ChipWhisperer is a trademark of NewAE Technology Inc., claimed in all jurisdictions, and registered in at least the United States of America, European Union, and Peoples Republic of China.
Tutorials derived from our open-source work must be released under the associated open-source license, and notice of the source must be clearly displayed. Only original copyright holders may license or authorize other distribution - while NewAE Technology Inc. holds the copyright for many tutorials, the github repository includes community contributions which we cannot license under special terms and must be maintained as an open-source release. Please contact us for special permissions (where possible).
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.